The next question is: what if we increase the pump rate above the threshold pump rate we discussed in the last section? Let’s consider two scenarios. In the first scenario, the pump rate is sitting at the threshold pump rate for a long time. Then, we abruptly increase the pump rate at time t = 0. This will lead to a rapid transient increase in the excited state population density $latex N_2$ and the gain $latex \gamma$. As a result, the round-trip gain will briefly exceed the round-trip loss, and the light will increase in intensity after each round trip. The increase in intensity will increase the stimulated emission rate, thus driving $latex N_2$ and $latex \gamma$ back down. This interplay of intensity and gain will exhibit damped oscillations as $latex N_2$, $latex \gamma$, and $latex I_{\nu}$ find their new steady-state values. These are called relaxation oscillations, and they’re sketched below.
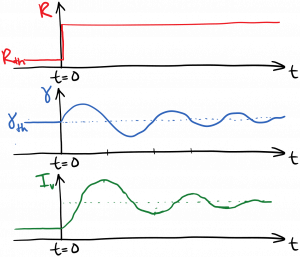
We can infer what the new steady-state values must be after the oscillations have ended. For one thing, the round-trip gain must equal the round-trip loss in steady state; otherwise the light intensity would increase or decrease indefinitely. Therefore, in steady state above threshold, the gain per length $latex \gamma$ must equal the threshold gain per length $latex \gamma_{th}$, regardless of the pump rate. This is called gain clamping. The gain is related to the inversion as $latex \gamma = \sigma(\nu) [N_2 – (g_2 / g_1) N_1]$, so therefore the inversion must also be clamped to its threshold value in steady state above threshold, $latex [N_2 – (g_2 / g_1) N_1] = \left[ N_2 – (g_2 / g_1) N_1 \right]_{th}$.
In the second scenario, we gradually increase the pump rate starting from zero, until we reach threshold, and then continue gradually increasing the pump rate above threshold. As long as the pump rate is increasing gradually, we won’t see the transient oscillations described above. Instead, the gain will increase with the pump rate until threshold is reached, at which point it will clamp. The light intensity increases very slowly with pump rate below threshold, and then increases rapidly with pump rate above threshold. This is diagrammed below, and discussed further below the diagram.
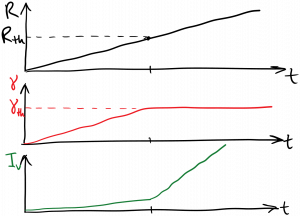
The gain clamping effect is an example of the gain saturation we described earlier. Far above threshold we can neglect spontaneous emission, as the pump and stimulated emission will be dominant. In steady state, as before we have the pump rate equal to the stimulated emission rate (minus the absorption):
$latex \displaystyle R = \frac{\sigma (\nu) I_{\nu}}{h \nu} \left[ N_2 – \frac{g_2}{g_1} N_1 \right]_{th} $
$latex \displaystyle = \frac{ \gamma_{th} I_{\nu}}{h \nu}$
For time t > 0, the pump rate on the left-hand side of this equation is greater than the threshold rate $latex R > R_{th}$ , so the right-hand side must also be greater than its threshold value. Since the gain is clamped above threshold, and the photon energy $latex h \nu$ doesn’t change with pumping, the intensity $latex I_{\nu}$ must increase to balance the equation. Solving for intensity far above threshold, we have
$latex \displaystyle I_{\nu} = \frac{h \nu R}{\gamma_{th}}$
Therefore, the intensity increases linearly with the pump rate in steady state above threshold.


You must be logged in to post a comment.