The Fabry-Perot cavity acts a bit like a leaky bucket – it stores a lot of optical energy at resonant wavelengths as the light bounces back and forth between the mirrors, but the light leaks out either side as well. In steady state, due to power conservation, the power being coupled into the cavity must equal the sum of the power exiting each mirror.
It is of interest to quantify ‘how good’ of a bucket the cavity is. To do this, we define the cavity Q as
$latex \displaystyle Q = 2 \pi \frac{\textrm{Optical energy stored in the cavity}}{\textrm{Optical energy lost in one cycle of oscillation}} $
or equivalently
$latex \displaystyle Q = 2 \pi \nu_0 \frac{\textrm{Optical energy stored in the cavity}}{\textrm{Rate of optical energy loss from cavity}} $
where $latex \nu_0$ is the center frequency of the resonant peak under consideration.
A high Q cavity is very good at storing energy – it stores a lot, and loses very little. Another definition, which is approximately equivalent for high-Q cavities, is
$latex \displaystyle Q = \frac{\nu_0}{\Delta \nu}$
where $latex \Delta \nu$ is the linewidth of the resonance (full width half maximum). The approximate equivalence of these two definitions means that the linewidth of a resonance is narrower if the loss from the cavity at that wavelength is small.
We can derive an approximate expression for the cavity Q of a Fabry-Perot resonator. The energy density stored in the electromagnetic field is
$latex \displaystyle u_{emag} = \frac{1}{2} \epsilon E^2 + \frac{1}{2} \mu H^2$
which we don’t actually need for this derivation, but I’m putting it here for reference. (We could use the fields calculated inside the cavity to evaluate this expression.) Suppose the energy density in the total forward wave in the cavity (sum of all rightward-propagating waves) is $latex u_{emag}^{fwd}$ and the energy density in the total backward wave is $latex u_{emag}^{bk}$. These two waves will constructively interfere at some points and destructively interfere at others (as shown in the Fabry-Perot field animations) but the total energy stored in the cavity has to be the same regardless:
$latex U_{emag} = (u_{emag}^{fwd} + u_{emag}^{bk}) (Area) L$
where “Area” is the cross-sectional area of the cavity. For high-reflectivity mirrors (high-Q cavity), the forward and backward waves will have approximately equal energy densities, so this becomes
$latex \displaystyle U_{emag} = 2u_{emag}^{fwd} (Area) L$
So that’s the numerator of our Q expression. For the denominator, we need to find the energy loss rate from the cavity. To assist with this, let’s use the following expression for the intensity (power/area) of the total forward wave in the cavity (assuming refractive index $latex n = 1$):
$latex I^{fwd} = \frac{c}{n} u_{emag}^{fwd}$
which we could derive using expressions we have for energy density and intensity. The fraction of this intensity which escapes the mirror is $latex (1 – R^2)$, where $latex R$ is the reflection coefficient of the mirror. Again, for a high-Q cavity, an approximately equal amount of light is lost from both mirrors, so the total rate of energy loss from the cavity is given by
$latex \displaystyle \frac{dU_{emag}}{dt} = – 2 (1 – R^2) \frac{c}{n} u_{emag}^{fwd} (Area) $
The magnitude of the right hand side of this equation is the denominator of our Q expression. Putting it together,
$latex \displaystyle Q = 2 \pi n \nu_0 \frac{L}{(1 – R^2) c}$
which can be rewritten as
$latex \displaystyle Q = \frac{2 \pi L}{\lambda (1 – R^2)}$
To test the equivalence of this expression to the other definition $latex Q = \nu_0 / \Delta \nu$, I calculated the $latex Q$ using both expressions for $latex R =0.8, 0.9$, and $latex 0.99$. The plots of the intensity within the cavity vs. frequency are given below, for reference. The percent different between the two expressions for these values of $latex R$ were $latex 20\%, 10\%$, and $latex 1\%$, respectively. As promised, the two definitions converge as the $latex Q$ increases.
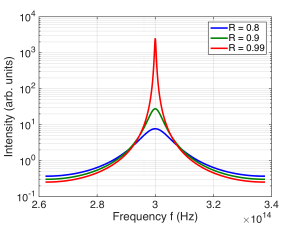
The Q factor for laser cavities can be very large, partly because $latex \nu_0$ is so large. As a result, a different quantity is occasionally used: the cavity finesse. First, let’s look at an expression for the resonant frequencies of the Fabry-Perot cavity. The condition for constructive interference within the cavity, and therefore resonant behavior, is $latex 2 L = m \lambda$. We can rewrite this as
$latex \displaystyle \nu = \frac{m c}{2 n L} $
Therefore, the frequency difference between resonances is $latex c / 2 n L$, which we call the free spectral range. The finesse is just defined as the free spectral range divided by the linewidth of the resonance:
$latex \displaystyle F = \frac{c / (2 n L)}{\Delta \nu}$


You must be logged in to post a comment.