We’re mostly interested in solutions to the Schrodinger equation for electrons bound to atoms or solids. In this case, the attractive electrostatic potential created by the nucleus traps low energy electrons in a three dimensional ‘box’ or cavity from which it can’t escape (without the addition of more energy). This potential well is diagrammed below.
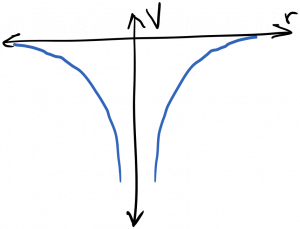
It’s useful to recall the Fabry-Perot cavity, and the effect it had on electromagnetic waves. In particular, remember that cavity resonances became sharper functions of frequency as the mirror reflectivity increased. As a general principle, as a wave’s confinement increases, the spectrum of the wave’s response becomes more sharply peaked. In the limit of a ‘perfect’ cavity which the waves can’t escape, only discrete resonant frequencies are allowed to persist within the cavity; waves at all other frequencies undergo total destructive interference and are therefore disallowed. The electrons bound to an atom are trapped in such a box; therefore, they can only occupy discrete energy (frequency) states. This is diagrammed below.

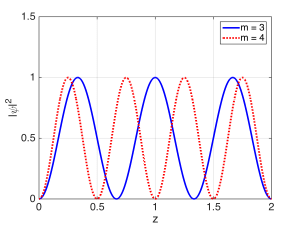
The condition for the resonant modes of the Fabry-Perot cavity was $latex 2 L = m \lambda$, which was the condition for constructive self-interference after multiple bounces. As the mirror reflectivities approached unity, we saw that the total wave inside the cavity became a mostly standing wave. The resonances could be classified according to the single ‘quantum number’ $latex m$, which was an integer. As $latex m$ gets bigger, there will be more half-wavelengths fitting between the mirrors, and therefore more peaks in the standing wave. The magnitude-squared of the field (or wavefunction) for two resonant modes (states) are shown below, with the quantum number $m$ labeled for each.
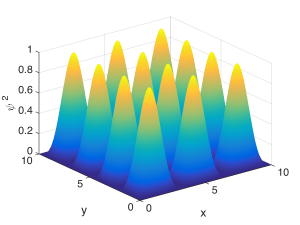
The Fabry-Perot cavity confines a wave in one spatial dimension – the direction perpendicular to the mirrors. If we instead confined the wave in two spatial dimensions, say $latex x$ and $latex z$, we’d have to fit half-wavelengths within the walls in each direction. This is depicted below. Hopefully you can see that describing these resonant modes would require two quantum numbers, one for each direction of confinement, describing how many peaks there were inside the box in each direction. For example, for the state shown below, one quantum number would be $latex m = 3$ and the other would be $latex q = 4$.
The electron waves in a Hydrogen atom (the simplest atom) are trapped in a 3d spherically-symmetric potential well. Describing the energy states of electrons in this box requires three quantum numbers, as the wave is confined in 3 spatial dimensions. Since the box is spherical, it makes more sense to use spherical coordinates. Thus, the first quantum number describes the number of $latex \psi^2$ peaks in the radial direction, and is called the principal quantum number $latex n$. $latex n$ can be any integer greater than zero.
The second quantum number describes the number of peaks in the angular $latex \phi$ direction, and is called the orbital quantum number $latex l$. $latex l$ is an integer greater than or equal to 0, and less than $latex n$: $latex 0 \leq l < n$. It might be a little odd imagining constructive interference happening in the $latex \phi$ direction, but you can visualize it as the wave needing to repeat itself as it goes $latex 2 \pi$ around the loop, as diagrammed below. $latex l = 0$ corresponds to a state with no angular variation in the wavefunction, so that it resembles a sphere. These are called $latex s$ states. $latex l = 1$ describes a state in which a single wavelength fits around the loop; these are called $latex p$ states. $latex l = 2$ states are called $latex d$ states; $latex l = 3$ states are called $latex f$ states. The state shown below has 10 half-wavelengths or 5 full wavelengths fitting around the loop and corresponds to $latex l = 5$. (Remember that a half-wavelength in $latex \psi$ looks like a full wavelength in $latex \psi^2$.)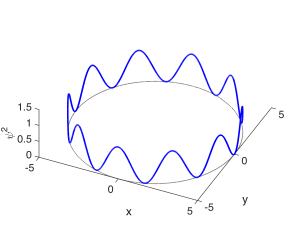
The third quantum number, which is the magnetic quantum number $latex m$, is a bit more complicated to understand, but is related to the orientation of this angular variation. $latex m$ can take positive or negative integer values whose magnitude is less than or equal to $latex l$: $latex |m| \leq l$.
There is a fourth quantum number $latex s = \pm 1/2$, but it’s associated with the spin of the electron, and not related to the spatial confinement.
Writing down the Schrodinger wave equation solutions for this case is beyond our scope, but there are plenty of great pictures available on the web. As usual, Wikipedia has some of the best. Check out this table: https://en.wikipedia.org/wiki/Atomic_orbital#Orbitals_table
For the Fabry-Perot cavity, each resonance had its own ‘quantum number’ $latex m$ and also its own wavelength and therefore frequency. This is also true for the electron states in an atom, which are called orbitals. Each state, which is described by a set of three quantum numbers, has its own frequency and therefore energy. Thus, there are discrete allowed energy states for electrons in atoms, as you’ve likely seen previously. The energy of the state depends strongly upon the principal quantum number $latex n$, for a simple reason: an electron sitting in a state with larger $latex n$ has a greater probability of being found at greater radii from the nucleus. Thus the approximate energy levels for electrons in a hydrogen atom are given by
$latex \displaystyle E_n = \frac{-13.6 eV}{n^2} $
which doesn’t depend on the other quantum numbers. This equation predicts considerable degeneracy: multiple energy states with different quantum numbers having the same energy. For example, if $latex n = 2$, there are four degenerate states corresponding to $latex l = 0$, $latex l = 1, m = 0$, and $latex l = 1, m = \pm 1$. However, energy splitting amongst these levels has been observed experimentally and can be calculated theoretically. Imposing an external magnetic field increases the energy splitting, as the various orbitals interact with the field differently depending on their relative orientation to the field.


You must be logged in to post a comment.