In equilibrium, the probability of an electron energy state in a semiconductor being occupied by an electron is given by the Fermi-Dirac distribution $latex f(E)$:
$latex \displaystyle f(E) = \frac{1}{1 + e^{(E-E_F) / k T}}$
where $latex E$ is the energy of the state we’re considering, and $latex E_F$ is called the Fermi energy. An electron state that sits at the Fermi energy has a 50% chance of being full. The Fermi-Dirac distribution is plotted for a few temperatures below.
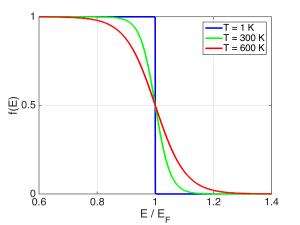
Note that states below the Fermi energy are generally full, while states above the Fermi energy are generally empty. We can think of the Fermi energy as the ‘fill level’ of the semiconductor, analogous to the fill level of a glass of water – below the fill level, the glass is full; above, empty. This is exactly true at zero temperature, but as the temperature increases, electrons are absorbing thermal energy in the form of phonons (lattice vibrations) and hopping out of low-energy states and into higher-energy states for brief periods. So at higher temperatures, a freshly-poured glass of beer or soda is a better analogy. Due to the bubbles and fizz near the top, there are some states below the fill line that are empty, and some states above the fill line that are full.
In a pure semiconductor, the valence band states are mostly full (occupied by electrons) and the conduction band states are mostly empty (not occupied by electrons). This means that the Fermi energy sits somewhere inside the band gap in a pure semiconductor, and in fact it sits near the middle of the band gap in most cases.
Because the valence band is almost always mostly full, it is more convenient to count the empty states in the valence band rather than the full ones. An empty valence band state is called a ‘hole’, and it effectively has a charge equal in magnitude and opposite in sign compared to an electron’s charge. A hole’s location moves around in the semiconductor if an adjacent electron ‘hops in’ to the hole, thereby effectively moving the hole to the location that was vacated by the electron. This is similar to the tile puzzles that you have probably seen, where you must rearrange the tiles to form a picture. You use your fingers to move tiles, but you are effectively moving the missing tile, or hole.
We often intentionally introduce impurities into the semiconductor, which is called ‘doping’. We do this in order to increase the number of electrons in the conduction band or holes in the valence band. If we replace an atom at some crystal lattice site with a different element that has one extra proton and one extra electron, the extra electron can be easily liberated from this ‘donor dopant’ to move about the conduction band, leaving behind a spatially fixed positive charge due to the extra proton. Similarly, introducing an ‘acceptor’ with one fewer electron and one fewer proton will liberate a hole to move around the valence band, leaving behind a fixed negative charge.
By introducing dopants, we can position the Fermi level higher or lower in the band gap, or even push it out of the band gap entirely. For example, introducing a large density of donor dopants will increase the number of electrons in the conduction band, meaning more conduction band states are filled. This pulls the Fermi level upwards in energy, so that a greater portion of the Fermi-Dirac distribution ‘tail’ overlaps with conduction band states.
When we move away from equilibrium (as we must to obtain inversion) the probability of energy state occupation may not be governed by the Fermi-Dirac distribution any longer. However, in many cases we can approximate the nonequilibrium electron and hole distributions with separate Fermi-Dirac distributions. In this case we define two quasi-Fermi levels, one for electrons in the conduction band, $latex F_n$, and one for holes in the valence band $latex F_p$. These quasi-Fermi levels act like the ‘fill levels’ for conduction band electrons and valence band holes, respectively. A conduction band state whose energy equals $latex F_n$ is 50% likely to be full, as is a valence band state whose energy equals $latex F_p$.


You must be logged in to post a comment.