A laser must have optical feedback, which doesn’t necessarily take the form of a Fabry-Perot cavity. However, a Fabry-Perot cavity is commonly used, so we’ll discuss it in a little more depth here.
You might recall that the resonant condition of the Fabry-Perot cavity is $latex 2 L = m \lambda$, where $latex L$ is the mirror separation. Light constructively interferes with itself at these wavelengths, and destructively interferes with itself at other wavelengths, so the cavity acts like a filter that selects these wavelengths; only those wavelengths of light are allowed to exist within the cavity (more accurately, a small range of wavelengths centered on those resonant wavelengths can exist, because the mirror reflection coefficients are less than one). The direction along the axis of the cavity (perpendicular to the mirrors) is called the longitudinal direction, and the allowed states of light inside the cavity are called modes, so the resonances that satisfy $latex 2 L = m \lambda$ are called the longitudinal modes of the cavity. As we saw when studying the Fabry-Perot interferometer, the light is mostly a standing wave within the cavity if the mirror reflectivities are near one, and the number of peaks of the light intensity between the mirrors is equal to the longitudinal mode number $latex m$.
However, the simple analysis of the Fabry-Perot cavity we’ve described doesn’t account for the other two spatial directions perpendicular to the longitudinal direction. The laser has finite size in the other two directions, called the transverse directions, so the optical beam inside the laser must also have finite extent in the transverse directions. Let’s discuss a few models of the light’s behavior which deal with all three spatial dimensions.
A simple model which is nonetheless very helpful for laser design is a ray-tracing model. Hopefully you have seen optical ray tracing in an introductory physics course. We treat the optical beam as a ray which travels in a straight line across the optical cavity, until it reflects at the mirror, where it obeys the law of reflection. As you can hopefully see in the diagram below, it is beneficial from this perspective to use concave spherical mirrors on either end of the laser cavity, in order to redirect light back towards the axis of the cavity, where the optical amplifier is located.
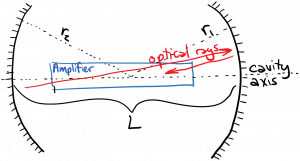
We say that an optical cavity is stable if the optical rays remain near the axis of the cavity after an indefinite number of round trips. It can be shown using ray tracing analysis that a cavity is stable if it obeys the following relation:
$latex \displaystyle 0 < g_1 g_2 < 1$
Oh look, we’re reusing the symbol $latex g$ once again! In this context,
$latex \displaystyle g_{1,2} = 1 – \frac{L}{r_{1,2}}$
and $latex r_1$ is the radius of curvature of spherical mirror 1.
In most situations we prefer a stable cavity, although there are exceptions to this rule. Note that a planar cavity will have $latex g_1 g_2 = 1$, which we classify as marginally stable: a ray that is traveling horizontally will stay near the axis, while any ray making an angle to the axis will gradually ‘walk off’ and diverge from the axis after several round trips.
In many cases, the optical beam within the cavity can be accurately modeled as a Gaussian beam. We saw the lowest-order Gaussian beam previously, which simply had a Gaussian intensity profile in the transverse directions. However, there also exist higher-order Gaussian beams, which exhibit more complex intensity patterns in the transverse directions. These are called the Hermite-Gaussian modes, and lovely pictures of the intensity patterns in the transverse directions can be found at the following link:
https://en.wikipedia.org/wiki/Gaussian_beam#Hermite-Gaussian_modes
Note that the transverse optical intensity pattern of these modes can be classified using two mode numbers. As you can see in the Wikipedia diagram, a mode number of 0 is associated with a single peak, 1 with two peaks, and so forth. The lowest-order Gaussian mode we discussed previously was the 00 mode. If there is a single intensity peak in the x direction and two peaks in the y direction, that is the 01 mode.
Bringing together all the mode numbers, a particular optical mode within the Fabry-Perot cavity can be described by a set of three mode numbers: the two transverse mode numbers, and the longitudinal mode number. In most cases the longitudinal mode number will be much higher, and the frequency separation between longitudinal modes is much smaller when compared to transverse modes, because the length of the cavity is generally much greater than the transverse dimensions of the beam (there are exceptions to this rule). If we stick with $latex m$ as the longitudinal mode number, and use $latex p$ and $latex q$ as the two transverse mode numbers, the spectrum of cavity modes might resemble the following sketch.



You must be logged in to post a comment.