Obtaining Inversion

As in the other laser types we’ve studied, it is necessary to obtain population inversion in order to have net optical amplification (stimulated emission dominant) rather than absorption.  However, since we now have bands of states rather than discrete states, what does inversion mean?  We don’t need to invert the entire bands, and in fact that would likely be impossible to achieve.  We only need to invert the energy states near the band edges, which will lead to amplification of photons whose energy is equal to the band gap.  Higher-energy states will not be inverted, and therefore higher-energy photons will still be absorbed, but that’s ok, because we only need to amplify a narrow range of photon energies (wavelengths).  This situation is diagrammed below.

As you can see in the diagram, we want states that are near the conduction band edge to have greater than a 50% chance of being full, and states near the valence band edge to have less than a 50% chance of being full.  Recall the definition of the quasi-Fermi levels: a conduction band state whose energy is equal to the electron quasi-Fermi level $latex F_n$ has a 50% chance of being full.  Conduction band states whose energy is greater than $latex F_n$ have less than 50% chance of being full, and conduction band states whose energy is less than $latex F_n$ have greater than 50% chance of being full.  The same applies to $latex F_p$ and valence band states.  Thus, a rule of thumb is: to achieve inversion, we must have the difference between the quasi-Fermi level energies be greater than the band gap energy, or

$latex \displaystyle F_n – F_p > E_G$

This is diagrammed below.

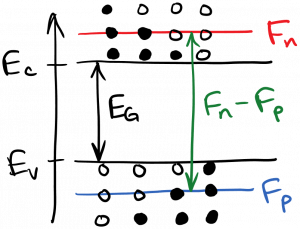
Of course, this situation can’t exist in equilibrium, as we only have a single Fermi level in equilibrium.  We must pump the semiconductor to a nonequilibrium state for inversion to be possible, which was also the case for the laser gain media we studied previously.