As we saw from Beer’s Law, in order to have optical amplification occur, we must have the density of atoms in the upper energy state $latex N_2 > (g_2 / g_1) N_1$, or if the degeneracies are equal to one, just $latex N_2 > N_1$. As previously mentioned, this is called inversion. Inversion requires pumping – an injection of energy into the atoms. This pumping could take many forms. In gas lasers, an electrical discharge is a common pumping mechanism. It is also possible to pump with light (optical absorption); however, if we are pumping with light, there must be at least one more atomic energy state involved besides $latex E_1$ and $latex E_2$ to make it work. Why?
Imagine we have a collection of atoms which are all initially in the lower energy state $latex E_1$. For simplicity, take $latex g_2 = g_1 = 1$. Let’s try to pump atoms into the upper energy state $latex E_2$ using a light source whose frequency $latex \nu = (E_2 – E_1) / h$. This will work fine initially – all the incoming light will be absorbed by the atoms in state 1, and those atoms will be promoted to state 2. However, as the density of atoms in state 2 $latex N_2$ climbs, eventually we will reach a point where $latex N_2 = N_1$. At this point, an incoming photon is equally likely to be absorbed or cause stimulated emission. Therefore, the light won’t be able to push $latex N_2$ any higher, at least in steady state. If we briefly manage to get $latex N_2 > N_1$, stimulated emission will dominate over absorption, and $latex N_2$ will be driven back down.
So, we must introduce a third energy state $latex E_3$ into our consideration. We could pump atoms from $latex E_1$ to $latex E_3$, as shown in the diagram below. We would be wise to choose a set of states for which there is a fast relaxation process that quickly drops atoms from state $latex E_3$ to $latex E_2$. In this way, $latex N_3$ will always be close to zero, and pump photons whose frequency $latex \nu_{pump} = (E_3 – E_1) / h$ will always be absorbed. At the same time, we would like atoms to linger in state $latex E_2$ a long time (a so-called ‘metastable’ state). If we satisfy these conditions, we can increase $latex N_2$ until it is greater than $latex N_1$ using the pump from $latex E_1$ to $latex E_3$. Once $latex N_2 > N_1$, we’ve achieved inversion and therefore amplification for photons whose frequency $latex \nu_{stim} = (E_2 – E_1) / h$.
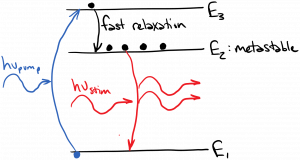
The three-level scheme above has a weakness. It is relatively easy to increase $latex N_2$, but we would also like to decrease $latex N_1$, in order to maximize the inversion $latex (N_2 – N_1)$. If the state $latex E_1$ is the ground state, the pump rate must be extremely large to lower $latex N_1$ significantly (a very intense pump would be required). One way to address this challenge is to introduce a fourth state into the pumping scheme, as diagrammed below. In this case, we want a pump tuned to the transition from $latex E_1$ to $latex E_4$, a fast relaxation process from $latex E_4$ to $latex E_3$, a fast relaxation process from $latex E_2$ to $latex E_1$, and a metastable state $latex E_3$. This scheme is designed to amplify light with frequency $latex \nu_{stim} = (E_3 – E_2) / h$. Atoms are pumped up to $latex E_4$ and quickly drop to $latex E_3$, where they linger. After a stimulated emission event drops the atom to state $latex E_2$, it quickly relaxes to state $latex E_1$, ensuring that $latex N_2$ will remain small. In this way, we can maximize the inversion $latex (N_3 – N_2)$.
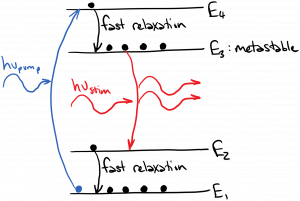
Of course, in engineering as in life, no improvement comes without a price. The 3- and 4-level pumping schemes make it easier to achieve a large inversion. The price we pay is an inherent loss of efficiency. If we are pumping with a single photon of energy $latex h \nu_{pump} = (E_4 – E_1)$, at best we will get out a single photon of energy $latex h \nu_{stim} = (E_3 – E_2)$. The energy difference $latex (h \nu_{pump} – h \nu_{stim})$ represents unavoidable energy loss in this system.


You must be logged in to post a comment.