In many lasers, the spectral width of the transition lineshape $latex g(\nu)$ and therefore the gain $latex \gamma(\nu)$ is greater than the free spectral range, which is the frequency separation between laser modes. This is diagrammed below. In this case, multiple optical modes may receive stimulated emission from a given atomic transition, and therefore multiple modes may be amplified. The question is, when the laser crosses threshold and begins lasing, will a single mode lase or will multiple modes lase?
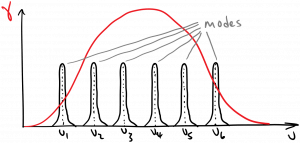
As you can see in the diagram, due to the frequency dependence of the gain, generally one mode will receive more gain than the others. As the pumping rate increases, the gain curve rises, until the round-trip gain equals the round-trip loss for one cavity mode. That mode begins to lase, and the gain at that frequency is clamped equal to the losses in steady state. This is diagrammed below. Generally speaking, most lasers will lase in a single mode when the pump rate equals the threshold pump rate, and for pump rates slightly above threshold. What happens when the pump rate is pushed far above threshold?
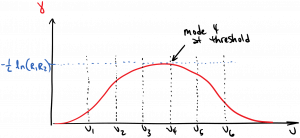
The answer depends on whether the gain is homogeneously or inhomogeneously broadened. In a homogeneously broadened medium, the gain spectrum can’t change shape, as all atoms are broadened in the same way. Therefore, once a single mode hits threshold, it will clamp the gain at that frequency, which will have the effect of clamping the gain curve at all frequencies, preventing other modes from lasing. From then on, it’s a “winner take all” scenario: all additional pumping only increases the number of photons in the single lasing mode. This is illustrated in the animation below, in which the pump rate R is increasing, and we watch the gain spectrum $latex \gamma(\nu)$ (red) and the intensity of three modes (green) evolve accordingly. (All quantities in the animation have arbitrary units, it is for illustration purposes only.)
However, in an inhomogeneously broadened medium, the gain spectrum is really a composite of gain spectra of different groups of atoms, whose gain may shift up or down relative to one another, thus changing the shape of the composite gain spectrum. When a single mode lases and clamps the gain curve at the mode frequency, the rest of the gain curve may continue rising as the pump is increased. Therefore multiple modes may achieve threshold and lase. For pump rates far above threshold, one may observe multiple ‘spectral holes’ burned into the gain curve, as the gain is clamped equal to the loss at each lasing mode frequency. This is illustrated in the animation below.


You must be logged in to post a comment.